UNDER CONSTRUCTION
Mean-Field Games (MFGs) is the study of games, whether they are subject to stochastic dynamics or not, in the limit when the number of agents tends to infinity. In this limit, any individual has a negligible effect on the population as whole., This allows one to solve for Nash equilibria in this mean-field limit by solving a stochastic control problem, in the presence of a mean-field measure flow, followed by a fixed-point problem for the mean-field measure flow itself.
The interest in such mean-field equilibria (MFE) stems from the fact that such MFE can often act as an approximation to the equilbria of N-player games — providing a so-called 
-Nash equilibria. The N-player game itself is extremely difficult to solve and often solving for strategies where agents do not have access to the states of other agents is often impossible. MFGs and the resulting MFE are easier to solve and side steps these issues.
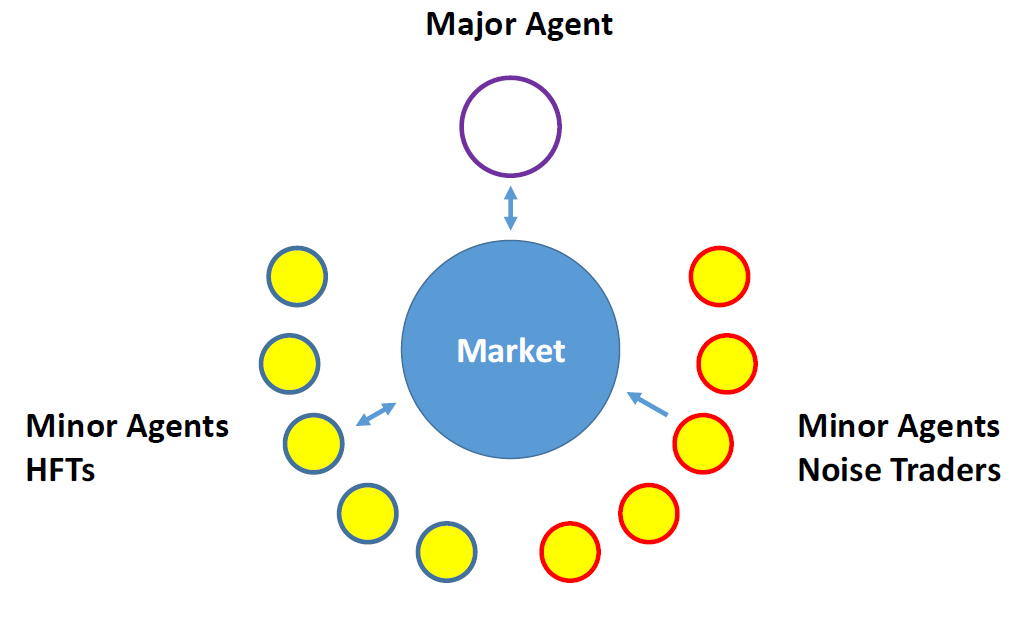
Some of my work in this area surrounds applying MFGs to algorithmic trading. In electronic trading venues, many agents are optimizing against the market and each other. Naturally, their individual actions also affect the market, and, therefore, while individual agents have a small effect on the environment, their aggregate effect does affect the rewards/costs of other agents. Hence, trading is a multi-player game, and we have used MFG techniques to analyze these problems.
Machine learning (ML) is widely used in a variety of fields where there are rich data sets. Its goal is to allow the data to “speak for itself” using minimal input or assumptions.
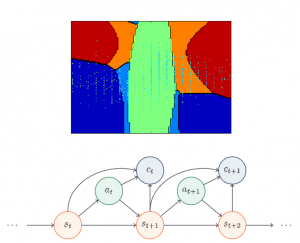
My research interest in ML is mostly in the domain of reinforcement learning (RL) and more specifically on risk-aware RL. When agents aim to optimize a criterion, while limiting risks, they are solving a stochastic control problem, since the future dynamics are unknown, and your actions affect it an unknown manner. One approach is to make model assumptions, such as dynamics are governed by controlled stochastic differential equations, that you then solve using methods of stochastic analysis and techniques from optimal stochastic control and stopping.
Another, model-agnostic, approach is to act on the system and see how it reacts, then use the reaction to update what you believe is optimal. This is the essence of RL, and it aims to find optimal actions in a model-agnostic manner. My interests lie in tying together stochastic analysis methods with ideas from reinforcement learning that lead to results which are robust and interpretable.
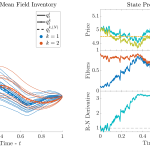
Traditionally, RL aims to optimize criterion that are expected discounted rewards and controlling for risk is done in ad-hoc manner. Rather, I am interested in making use of the notion of time-consistent dynamic risk measures that from the outset lead to optimal policies that are time-consistent and explicitly incorporate risk into the criterion.
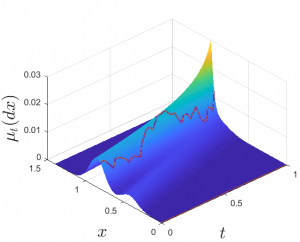
I am interested in how stochastic control and reinforcement learning techniques can assist with making optimal decisions in the context of clean energy. One prime example of this is the offset credit (OC) markets. In these markets, regulated firms must either acquire OC certificates, through purchasing from other agents, or generate OC certificates, by, e.g., engaging in clean projects like planting trees. As OC are generated, they impact the OC prices (as this increases their supply), similarly buying and selling OCs could affect impact their price.
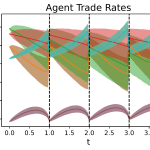
Understanding how to model, and then optimise decisions is a non-trivial task that stochastic control and reinforcement learning can assist in shedding important light on. As well, posing these problems as principal-agent games, where the principal is viewed as the regulator and the agents those who are active in the OC markets, can inform regulators what are the best policies to implement to induce the kind of behaviour they wish to induce in the agents.
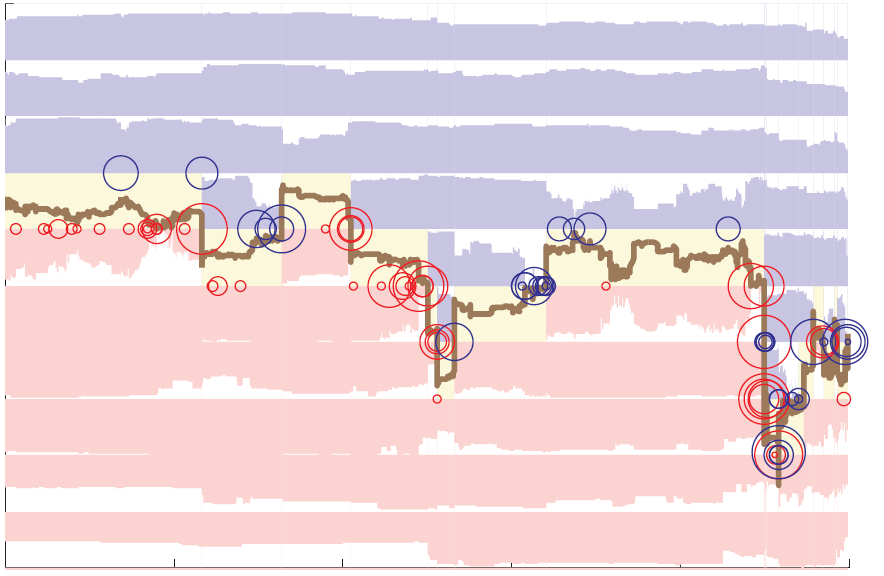Algorithmic trading generally refers to the automatic trading of assets using a predefined set of rules. These rules can be motivated by financial insights, and/or mathematical and statistical analysis of assets. Price, order-flow, and posted liquidity are often factors in determining how to trade. When decisions are made at ultra-fast time scales, and mostly rely
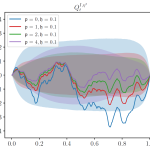
My research in this arena has focused on the application of stochastic control and reinforcement learning techniques to pose and solve a variety of algorithmic and high-frequency trading problems. One example is how to incorporate both limit and market orders into optimal execution problems to reduce the total execution cost. These problems lead to interesting combined optimal stopping and control problems.