-
- Page 33. Third displayed equation and text should be:
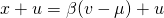 As
As and
and 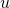 are independent and normal,
are independent and normal, 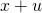 is normal with mean
is normal with mean 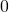
- Page 33. Fourth displayed equation, and sentence that follows should read:
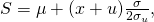
so that the linear sensitivity parameter is
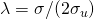 .
. - Page 36. First sentence in paragraph preceding 2.3.1 should read: In later chapters we show how trading algorithms are built to either take advantage of informational advantages or to adjust the depth at which LOs are posted to recover losses from trading with more informed traders.
- Page 37: the
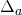 in
in 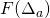 in the denominator should be
in the denominator should be 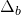 . This is the right equation
. This is the right equation
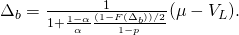
- Pages 110-111. The equations below (5.21) onwards should be
-
- Page 111, the inequality in point (ii) should be
 NOT
NOT 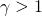 . For
. For 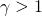 , there is an upper bound on wealth, rather than a lower bound.
, there is an upper bound on wealth, rather than a lower bound. -
In the exercises of Chapter 6 the liquidation penalty has the same typo inthree places. The penalty is not ‘minus‘
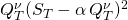 it should be ‘plus‘
it should be ‘plus‘ 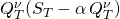
The typos appear in first displayed equation in E.6.1, and equations (6.41) and (6.47) - Page 175. There is a minus sign missing in equation (7.22) . The equation should be:
![Rendered by QuickLaTeX.com h_1(t,\mu) = b\,\mathbb{E}_{t,\mu}\left[ \int^T_t \left( \frac{\zeta e^{\gamma (T-u)}- e^{-\gamma (T-u)} }{\zeta e^{\gamma (T-t)}-e^{-\gamma (T-t)} } \right) \,\mu_u\,du \right]\,.](https://sebastian.statistics.utoronto.ca/wp-content/ql-cache/quicklatex.com-2a2785e6000bb746e363ed0cab00ec90_l3.png)
- Equations (A.8), (A.11), (A.17), and (A.18) are all missing the term
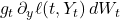 . This change does NOT, however, alter the corresponding differential operators, as this term represents a martingale increment.
. This change does NOT, however, alter the corresponding differential operators, as this term represents a martingale increment.
- Page 33. Third displayed equation and text should be:
Feel free to contact us if you find any. If you can, please use the following format
Section:
Page:
Equation/figure/table number:
The error is:
Also, we prefer it if you send the maths in LaTeX format
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} 0= &\left( \partial_t + r\,x\,\partial_x +(\mu-r)\,S\,\partial_S+ \tfrac{1}{2}\,\sigma^2\,S^2\,\partial_{SS}\right) H \\ &+ \sup_\pi\left\{ \pi \,\left( (\mu-r)\,\partial_x +\sigma^2\,S\,\partial_{xS}\right) H + \tfrac{1}{2}\sigma^2\,\pi^2\,\partial_{xx}H\right\}\,,\\[1em] \end{split} \end{equation*}](https://sebastian.statistics.utoronto.ca/wp-content/ql-cache/quicklatex.com-ce854135e606e9887f77824c98ee0394_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split} &\pi \,\left( (\mu-r)\,\partial_x +\sigma^2\,S\,\partial_{xS}\right) H + \tfrac{1}{2}\sigma^2\,\pi^2\,\partial_{xx}H\\ &\quad =\tfrac{1}{2}\,\sigma^2\,\partial_{xx}H \left(\left(\pi - \pi^*\right)^2 - (\pi^*)^2 \right)\;,\\[1em] \end{split} \end{equation*}](https://sebastian.statistics.utoronto.ca/wp-content/ql-cache/quicklatex.com-7ce17fa4b537e88848cd827e4afd28f0_l3.png)